Problemas

Distribución binomial

Para una variable aleatoria con distribución binomial \(X \sim binom(x, n=10, p=0.5)\) . Determine: la función de distribución asociada a \(X\).

\(P(X = 5)\)

dbinom(5,10,0.5)

[1] 0.2460938

\(P(X \leq 2)\)

pbinom(2,10,0.05)

[1] 0.9884964

\(P(3\leq X <5)\)

dbinom(3,10,0.05)+dbinom(4,10,0.05)

[1] 0.01143987

pbinom(4,10,0.05)-pbinom(2,10,0.05)

[1] 0.01143987

\(P(X\geq 8)\)

pbinom(7,10,0.05, lower.tail = FALSE)

[1] 1.605078e-09

1-pbinom(7,10,0.05)

[1] 1.605078e-09

Construya la gráfica de \(f_{_{X}}(x)\)

library(ggplot2)
x=0:10
fx=dbinom(x,10,0.05)
dat=data.frame(x,fx)
ggplot(dat) + geom_point(aes(x, fx),colour = c2, size = 3) +
  scale_x_continuous(limits = c(0, 10),
                     breaks = 0:10)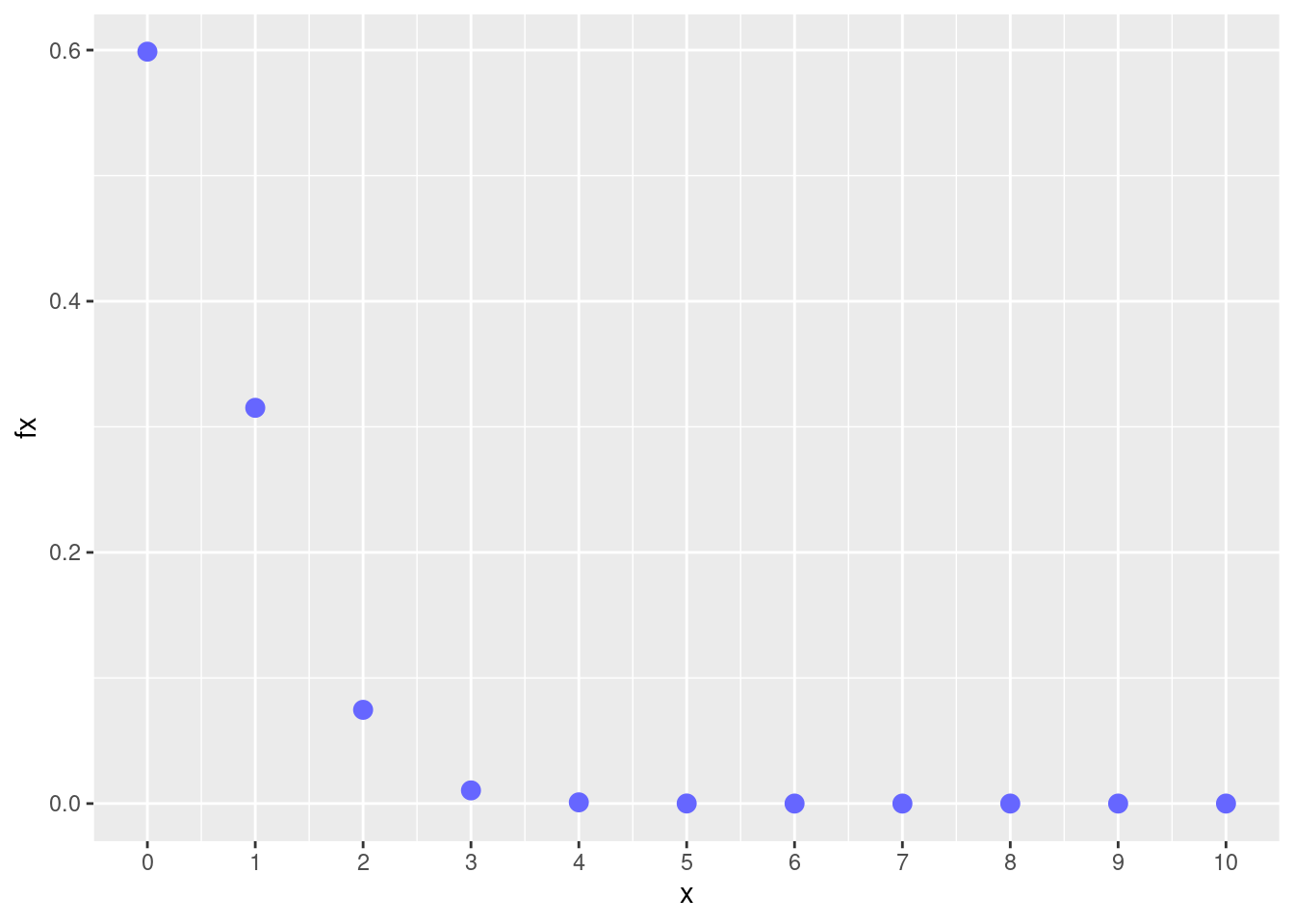

Distribución Poisson

Suponga que X tiene una distribución Poisson con media \(\lambda=4\) (\(X \sim pois(x,\lambda=4)\)). Determine:

\(P(X = 0)\)

# Distribución Poisson
# X :  número de  eventos que ocurren por unidad de tiempo, longitud, superficie o volumen
# f(x)       dpois(x, lambda)
# F(x) =P(X<=x) ppois(q, lambda, lower.tail = TRUE)
# Percentil  qpois(p, lambda, lower.tail = TRUE)
# aleatorio  rpois(n, lambda)

dpois(0,4)

[1] 0.01831564

\(P(X = 4)\)

dpois(4,4)

[1] 0.1953668

\(P(X \geq 2)\)

ppois(1,4,lower.tail = FALSE)

[1] 0.9084218

\(P(X \leq 2)\)

ppois(2,4)

[1] 0.2381033

Construya la gráfica de \(f_{_{X}}(x)\)

library(ggplot2)
x=0:15
fx=dpois(x,4)
dat=data.frame(x,fx)
ggplot(dat) + geom_point(aes(x, fx),colour = c2, size = 3) +
  scale_x_continuous(limits = c(0, 15),
                     breaks = 0:15)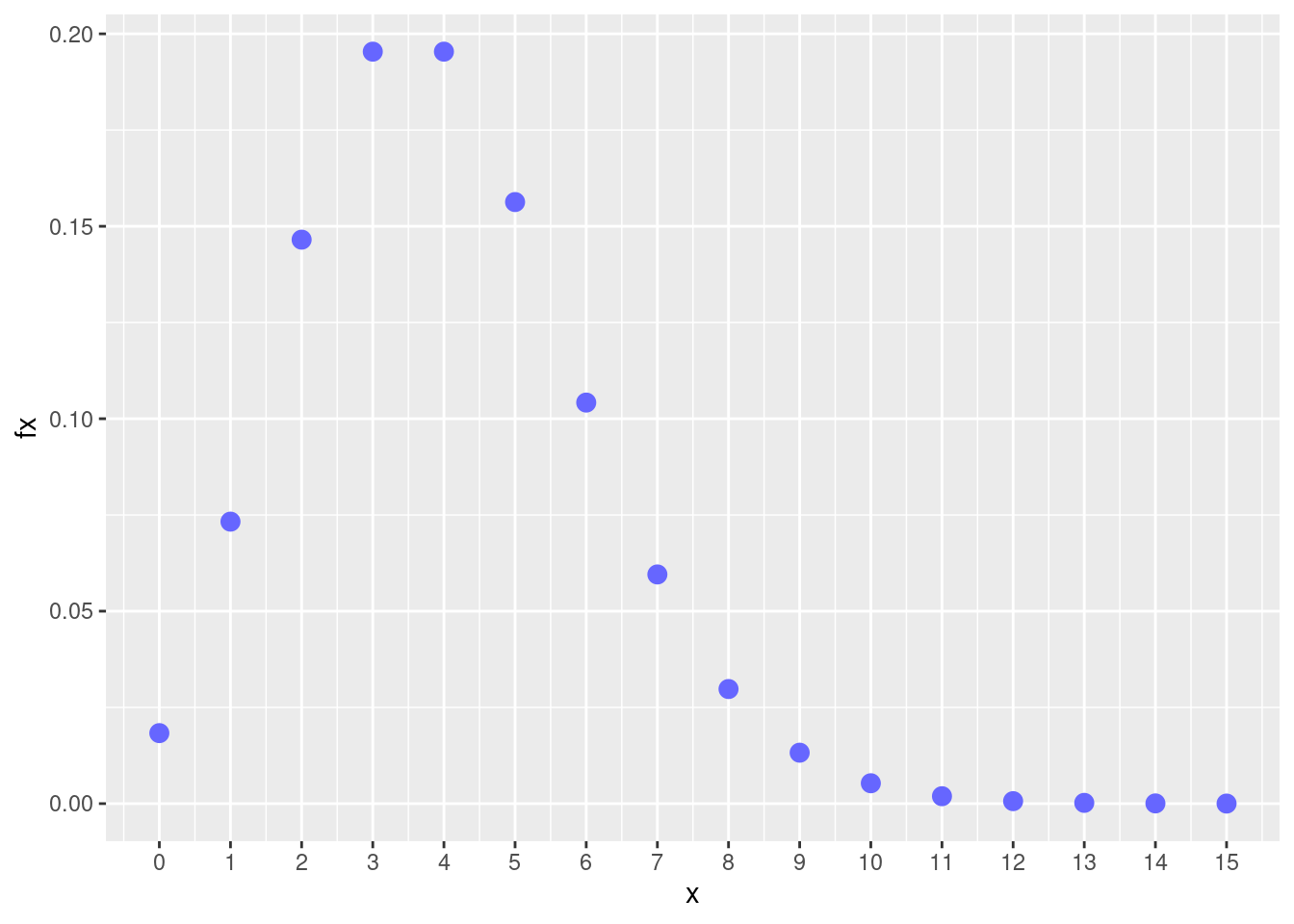

Distribución geométrica

Sea una variable geométrica \(X\sim geomn,(x,p=0.05)\)

\(P(X = 1)\)

dgeom(1,0.05)

[1] 0.0475

\(P(X \leq 2)\)

pgeom(2,0.05)

[1] 0.142625

\(P(X =8)\)

dgeom(8,0.05)

[1] 0.03317102

\(P(X\geq 2)\)

1-pgeom(1,0.05)

[1] 0.9025

Construya la gráfica de \(f_{_{X}}(x)\)

library(ggplot2)
x=0:20
fx=dgeom(x,0.05)
dat=data.frame(x,fx)
ggplot(dat) + geom_point(aes(x, fx),colour = c2, size = 3) +
  scale_x_continuous(limits = c(0, 20),
                     breaks = 0:20)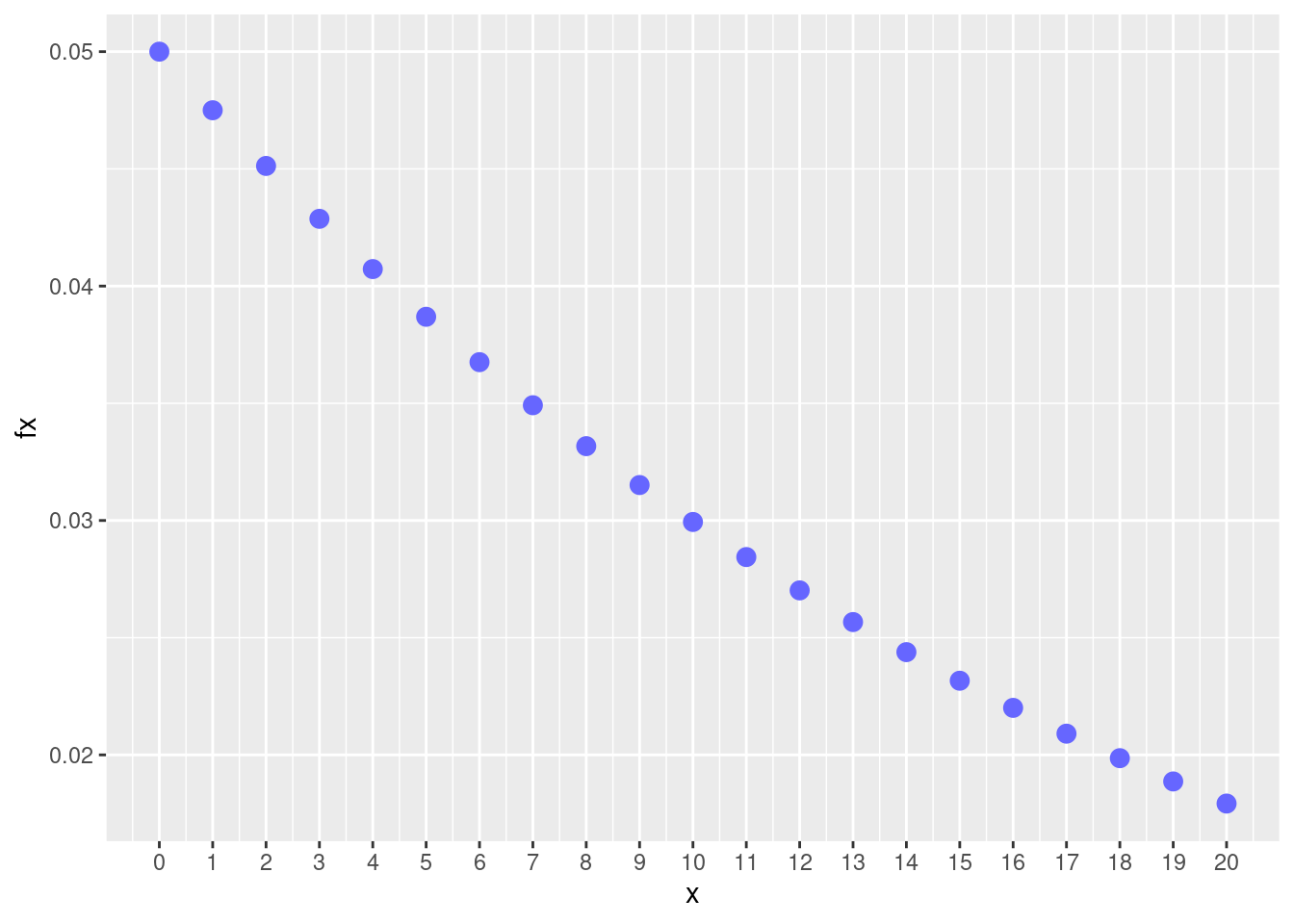

Distribución hipergeométrica

Suponga que X tiene una distribución hipergeometrica con \(N=100\), \(n=4\) y \(K=20\). (\(X\sim hyper(x,N=100,n=4,k=20)\)) Determine:

\(P(X = 1)\)

# dhyper(x, m, n, k, log = FALSE)
# dhyper(x, N-K, K, (n), log = FALSE)
  
dhyper(1,80,20,4)

[1] 0.02325804

\(P(X = 3)\)

dhyper(3,80,20,4)

[1] 0.4190527

\(P(X \geq 1)\)

1-phyper(0,80,20,4)

[1] 0.9987644

1-dhyper(0,80,20,4)

[1] 0.9987644

phyper(0,80,20,4, lower.tail = FALSE)

[1] 0.9987644

\(P(X = 4)\)

dhyper(4,80,20,4)

[1] 0.4033382

Construya la gráfica de \(f_{_{X}}(x)\)

library(ggplot2)
x=0:4
fx=dhyper(x,80,20,4)
dat=data.frame(x,fx)
ggplot(dat) + geom_point(aes(x, fx),colour = c2, size = 3) +
  scale_x_continuous(limits = c(0, 4),
                     breaks = 0:4)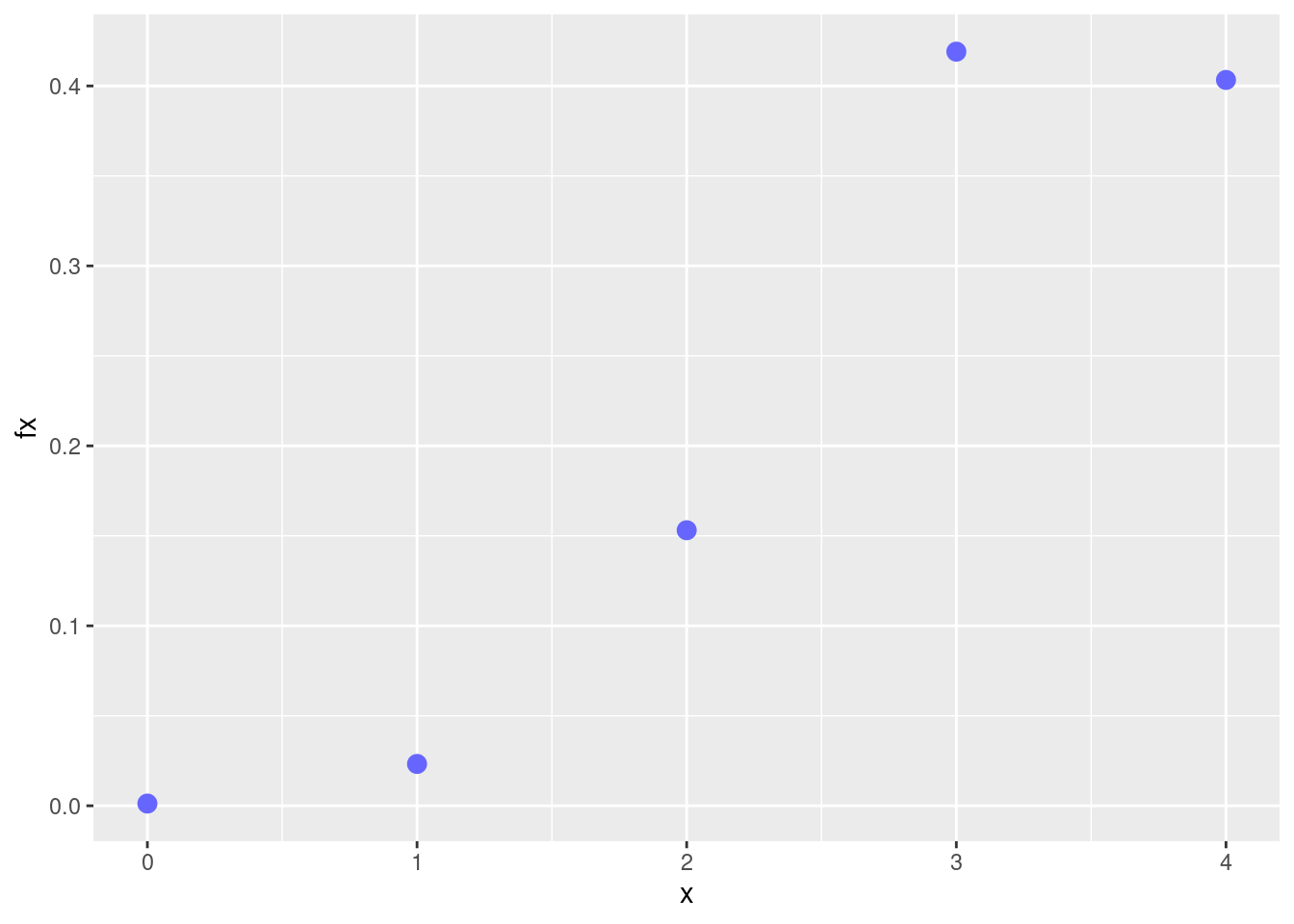

Nota: En este caso se debe realizar una conversión de los parámetros para utiliar la función dhyper de R m = K, número de éxitos en la urna N = m + n , total de elementos en la urna K = n, tamaño de la muestra a extraer de la urna

Para este caso : m=20, n=80, k=4

Distribución binomial negativa

Sea la variable \(X\) con distribución binomial negativa con N=100 , K=20, n=5 (\(X\sim nbinom(x,n,p,mu)\) )

\(P(X = 0)\)
\(P(X = 6)\)
\(P(X \geq 10)\)
\(P(X \leq 12)\)
E[X] y V[X]
Construya la gráfica de \(f_{_{X}}(x)\)

library(ggplot2)
x=0:40
fx=dnbinom(x,5,20/100)
dat=data.frame(x,fx)
ggplot(dat) + geom_point(aes(x, fx),colour = c2, size = 3) +
  scale_x_continuous(limits = c(0, 40),
                     breaks = 0:40)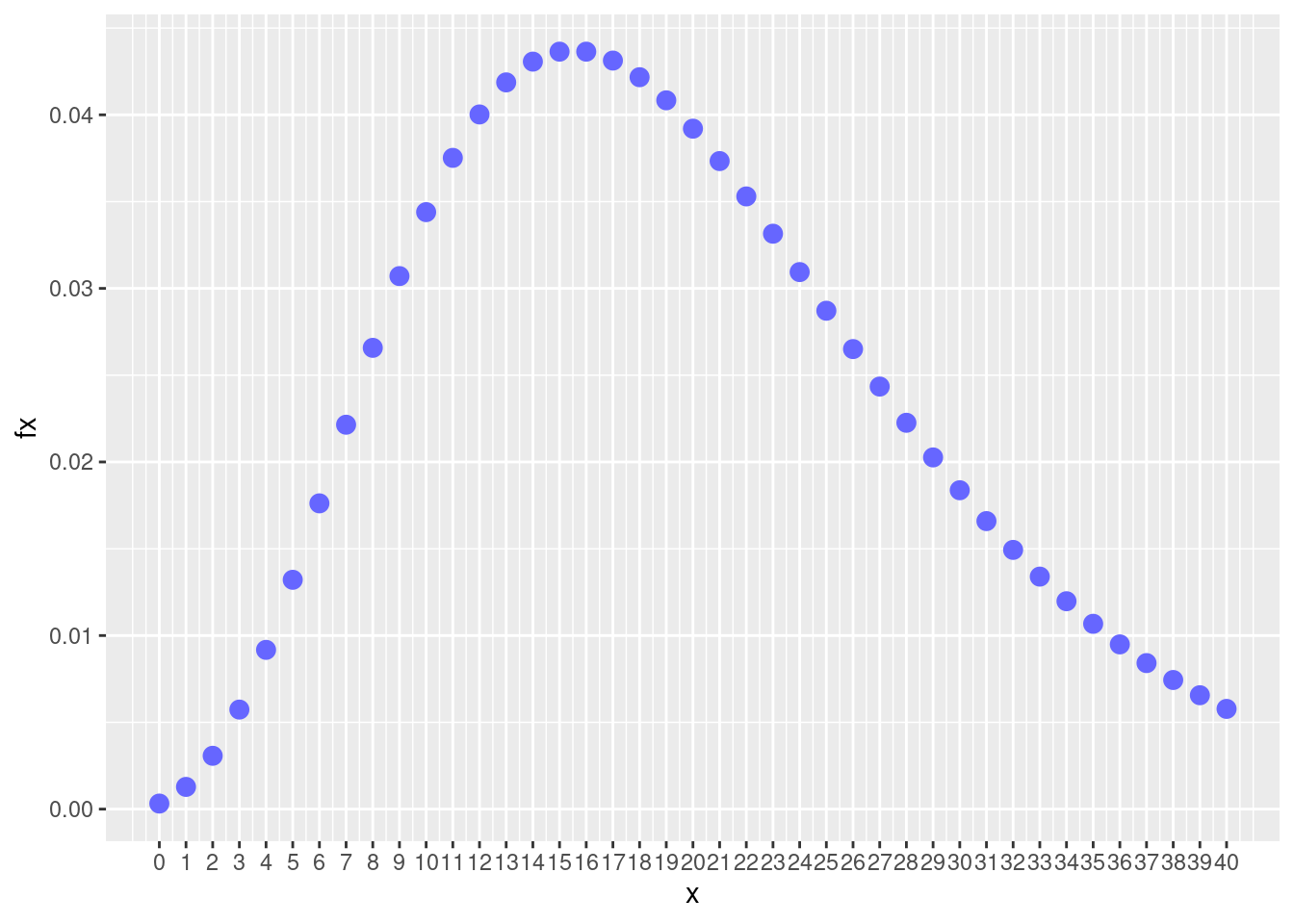

En un cargamento grande de llantas para automóviles, el 5% tiene imperfecciones. Se eligen de manera aleatoria 4 llantas para ser instalada en un automóvil. (Sea X el número de llantas con imperfecciones. \(X \sim binom(n=4, p=0.05\) )

¿ Cuál es la probabilidad de que ninguna de las llantas tenga imperfecciones?

# X: numero de llantas con imperfecciones
dbinom(0,4,0.05)

[1] 0.8145062

¿ Cuál es la probabilidad de que sólo una de las llantas tenga imperfecciones?

dbinom(1,4,0.05)

[1] 0.171475

¿ Cuál es la probabilidad de una o más llantas tenga imperfecciones?

1-dbinom(0,4,0.05)

[1] 0.1854938

pbinom(0,4,0.05, lower.tail = FALSE)

[1] 0.1854938

Problemas propuestos

Los clientes llegan al mostrador de una tienda de acuerdo con una variable aleatoria Poisson con una frecuencia promedio de ocho clientes por hora.(\(\lambda=8\))

Calcule la probabilidad de que entre las 8 AM y las 9 AM lleguen exactamente cinco clientes.

dpois(5,8)

[1] 0.09160366

Calcule la probabilidad de que entre las 2:30 PM y las 3:30 PM no lleguen más de tres clientes.

ppois(3,8)

[1] 0.04238011

Calcule la probabilidad de que lleguen exactamente dos clientes dentro de un intervalo de dos horas continuas, por ejemplo entre 10 AM y 12 M.

dpois(2,8*2)

[1] 1.44045e-05

Calcule el valor esperado del número de personas que llegan a la tienda entre las 2 PM y las 4:30 PM.

8*2.5

[1] 20

Se está desarrollando una nueva variedad de maíz en una extensión de experimentación agrícola. Se espera que tenga una tasa de germinación del 90%. Para verificar esto, se plantan 20 semillas en suelos de idéntica composición y se les dedican los mismos cuidados. Si la cifra 90% es correcta, ¿cuántas semillas se espera que germinen? Si sólo germinan 15 o menos, ¿hay razón para sospechar de la cifra 90%?

pbinom(15,20,0.90)

[1] 0.0431745

Se sabe que 3% de las personas a las que se les revisa el equipaje en un aeropuerto lleva objetos cuestionables. ¿Cuál es la probabilidad de que una serie de 15 personas cruce sin problemas antes de que se atrape a una con un objeto cuestionable? ¿Cuál es el número esperado de personas que pasarán antes de que se detenga a una?

 dgeom(15,0.03)

[1] 0.01899754

El esquema de aceptación para comprar lotes que contienen un número grande de baterías consiste en probar 75 baterías seleccionadas al azar y rechazar el lote completo si falla una sola o más baterias. Suponga que la probabilidad de encontrar una que falle es de 0.01.

¿Cuál es la probabilidad de que se acepte un lote?

1-dbinom(0,75,0.01)

[1] 0.5294134

pbinom(0,75,0.01,lower.tail = FALSE)

[1] 0.5294134

¿Cuál es la probabilidad de que se rechace un lote en la vigésima prueba?

pgeom(9,0.01, lower.tail = FALSE)

[1] 0.9043821

¿Cuál es la probabilidad de que se rechace en 10 o menos pruebas?

pgeom(10,0.01)

[1] 0.1046617

Una aereolinea nacional tiene aviones de 100 asientos para el servicio de transporte nacional. Se estima que la probabilidad de que una persona llegue al vuelo es de 0.90, debido a lo cual la aereolinea vende 105 tiquetes con el fin de minimizar la partida de aviones con sillas vacías. ¿cuál es la probabilidad de que todas las personas que lleguen para abordar el avión tengan asiento?

pbinom(100,105,0.90, lower.tail = FALSE)

[1] 0.01671632

El número de grietas en un pavimento se estima en guna rieta por cada 100m en promedio(\(\lambda=1\)) . Se desea estimar la probabilidad de:

Halla exactamente 8 grietas en una longitud de 500 m

dpois(8,1*5)

[1] 0.06527804

No se presente ninguna grieta en 100 m

dpois(0,1)

[1] 0.3678794

Se presenten menos de 2 grietas en 500 m

ppois(1,1)

[1] 0.7357589

Un científico inocula a varios ratones, uno a la vez, el virus que produce una enfermedad, hasta que encuentra a 2 que contraen la enfermedad. Si la probabilidad de contraer la enfermedad es de 1/6, ¿cuál es la probabilidad de que tenga que inocular a 8 ratones?

Resumen

binomial

\(X \sim binom\) cuando procede de un experimento binomial

El experimento consta de \(n\) ensayos
Cada ensayo tiene solo dos posible resultados: éxito (E) o fracaso (F) (experimento Bernoulli),
La probabilidad de éxito es igual a \(p\) y se mantiene fija para todos los ensayos P(E). La probabilidad de fracaso es \((1-p)=q\),
Los ensayos son independientes,
La variable objeto de estudio \(X\), corresponde al número de éxitos obtenidos en los \(n\) ensayos.
Se puede decir que la suma de \(n\) variables independientes con distribución Bernoulli(\(p\)), se distribuye de manera Bionomial(\(n,p\))

Poisson

\(X \sim poiss\), cuando representa el número de eventos que ocurren en un espacio de tiempo, distancia, area, volumen

geométrica

\(X \sim geom\), cuando representa el número del ensayo donde ocurre el primer éxito (En R representa el número de fracasos)

hipergeométrica

\(X \sim hyper\), cuando representa el número de exitos que se pueden obtener al extraer una muestra de tamaño \(n\), de una urna que contiene \(N\) objetos de los cuales \(K\) corresponden a exitos.

binomial negativa

\(X \sim nbinom\), cuando representa el número del ensayo donde ocurre el \(r\)-simo ensayo (En R representa el número de fracasos para encontrar r éxitos)

Código R

modelo	\(F(x)\)	\(X_{p}\)	\(f(x)\)	aleatorio
binomial	pbinom	qbinom	dbinom	rbinom
gometrico	pgeom	qgeom	dgeom	rgeom
hipergeometrico	phyper	qhyper	dhyper	rhyper
Poisson	ppois	qpois	dpois	rpois
binomial negativo	pnbinom	qnbinom	dnbionom	rnbinom

Taller Modelos especiales discretos

dgonzalez80