Para el desarrollo del Módulo 3, requerimos poder evaluar y representar funciones de variables tanto discretas como continuas.



Caso discreto


Supongamos que \(X\) es una variable aleatoria discreta con función de distribución de probabilidad dada por :

\(f(x)=\displaystyle\binom{10}{x} 0.60^{x} 0.40^{10-x}\), para \(x = 0,1,2,3,4,5,6,7,8,9,10\)



x=0:10
fx=choose(10,x)*0.60^x*0.40^(10-x)

Para verificar que es una función de distribucion de probabilidad sumamos todos sus valores

sum(fx)
[1] 1

Para representar gráficamente la función utilizamos la función plot

x=0:10
fx=choose(10,x)*0.60^x*0.40^(10-x)  
plot(x,fx, las=1, ylab="f(x)", xlab="número personas que asisten", pch=19)
lines(x, fx, type="h", col=2)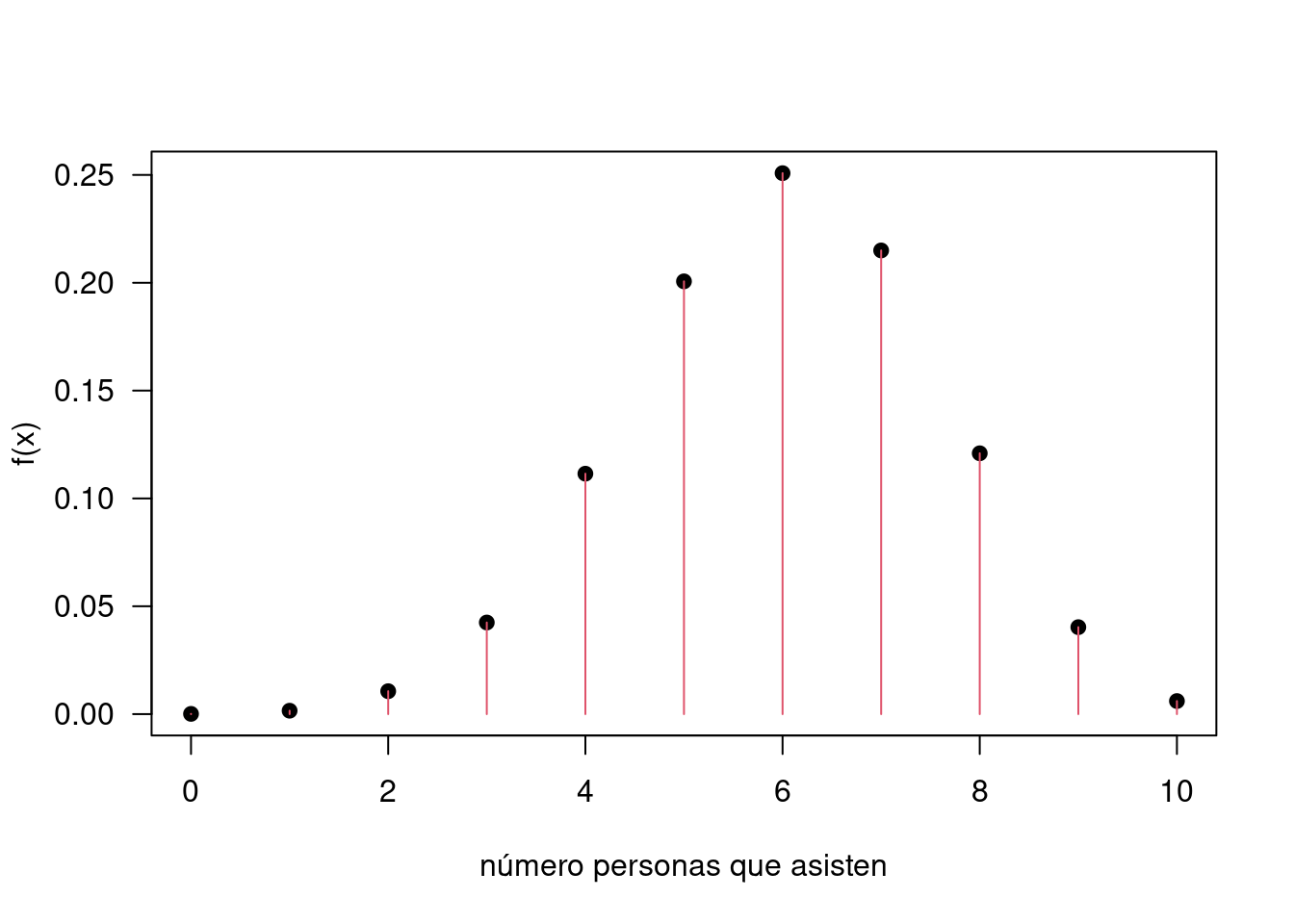



Tambien podemos utilizar el paquete ggplot2 

library(ggplot2)
x=0:10
fx=choose(10,x)*0.60^x*0.40^(10-x)  
dat=data.frame(x,fx)
ggplot(dat) + geom_point(aes(x, fx),colour = "orange", size = 4) +
  scale_x_continuous(limits = c(0, 10),
                     breaks = c(0,1,2,3,4,5,6,7,8,9), 
                     labels = c('0','1','2','3','4','5','6','7','8','9'))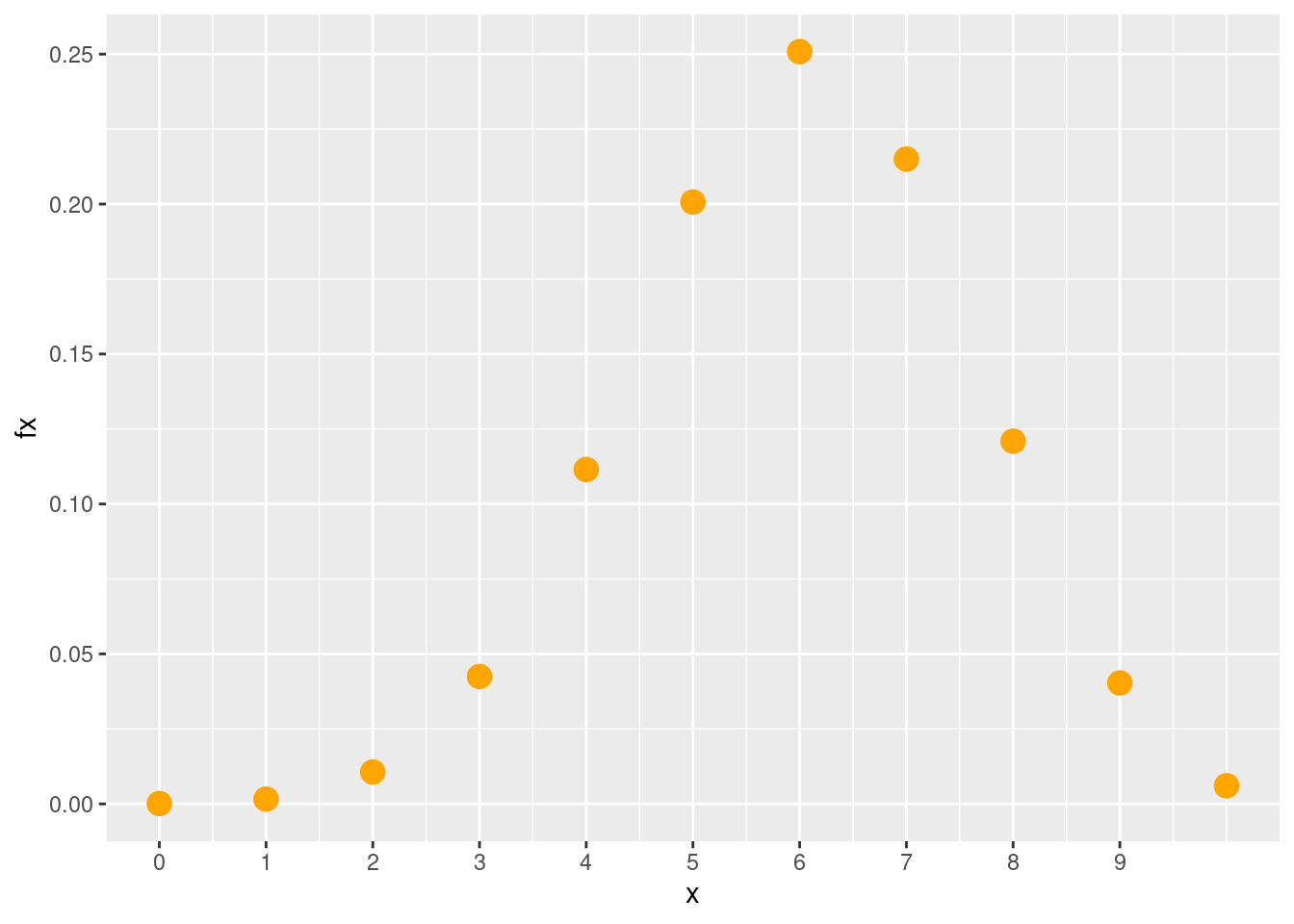



Tambien podemos construir una tabla con las probabilidades asignadas a cada valor de \(X\) 

x=0:10
fx=choose(10,x)*0.60^x*0.40^(10-x)  
Fx=cumsum(fx)
dt=data.frame(x,fx,Fx)
dt
    x           fx           Fx
1   0 0.0001048576 0.0001048576
2   1 0.0015728640 0.0016777216
3   2 0.0106168320 0.0122945536
4   3 0.0424673280 0.0547618816
5   4 0.1114767360 0.1662386176
6   5 0.2006581248 0.3668967424
7   6 0.2508226560 0.6177193984
8   7 0.2149908480 0.8327102464
9   8 0.1209323520 0.9536425984
10  9 0.0403107840 0.9939533824
11 10 0.0060466176 1.0000000000



Nota: En este caso \(\binom{n}{k}\), corresponde a la combinatoria de \(n\) con \(k\), que representa el número de maneras diferentes como se puede seleccionar una muestra de tamaño \(k\) de una urna que contiene \(n\) elementos son importar el orden y sin repetición.

Caso continuo



Gráficos

Las variables aleatorios continuas requieren el uso de integrales y por tanto su representación gráfica corresponde a una área bajo la \(f(x)\)



curve(1/4*exp(-x/4) , from=0, to=20, n=300, xlab="x", ylab="f(x)", 
             col="blue", lwd=3, main="f(x)=1/4*exp(-x/4)", las=1  )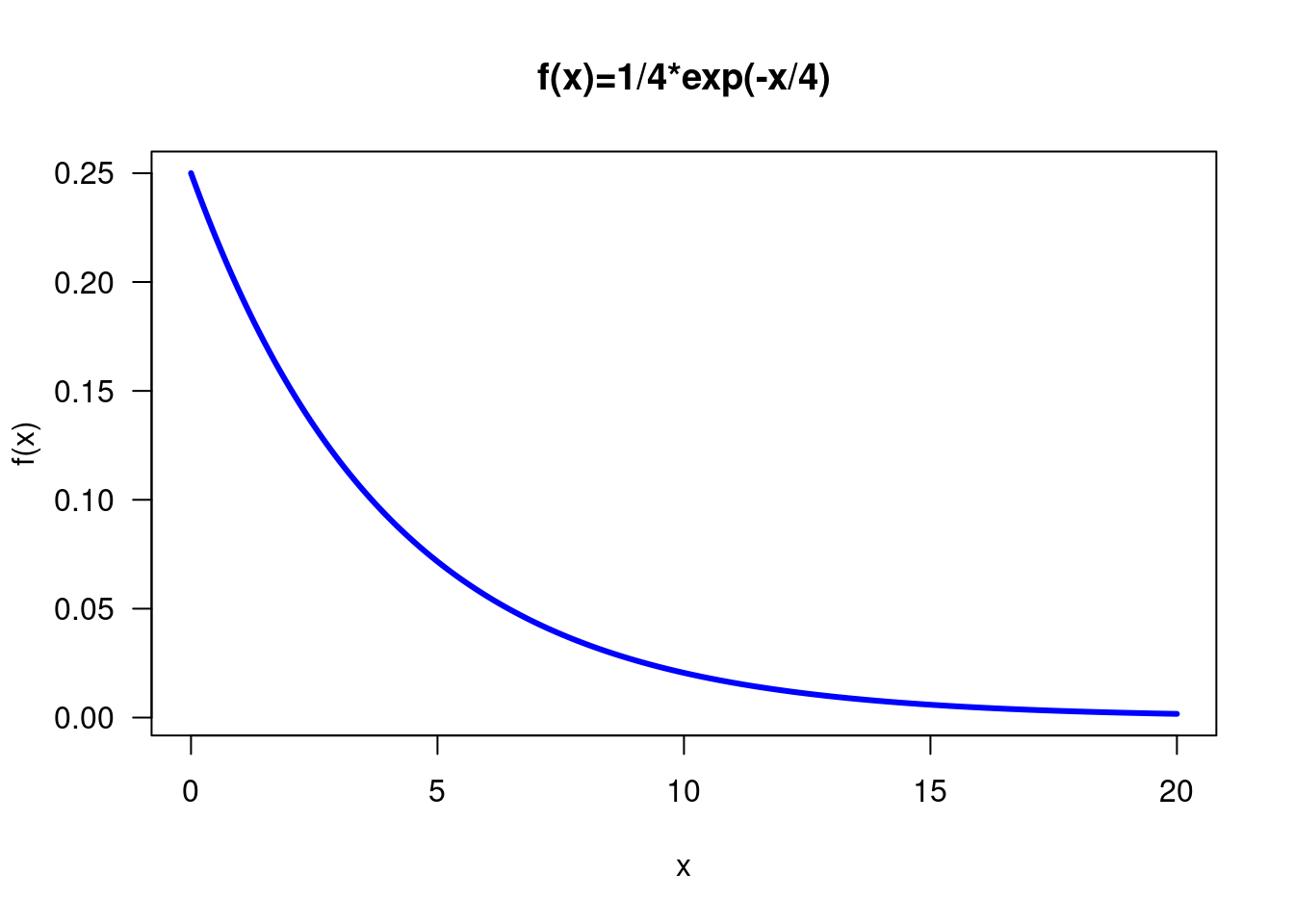


x=seq(from = 0, to = 20, by = 0.1)
y=function(y){1/4*exp(-y/4)}
fx=y(x)
plot(x,fx, xlab="x", ylab="f(x)", type="l",
             col="blue", lwd=3, main="f(x)=1/4*exp(-x/4)", las=1  )
x1=c(0,x,0)
fx1=c(0,fx,0)
polygon(x1, fx1,col = "#1b98e0")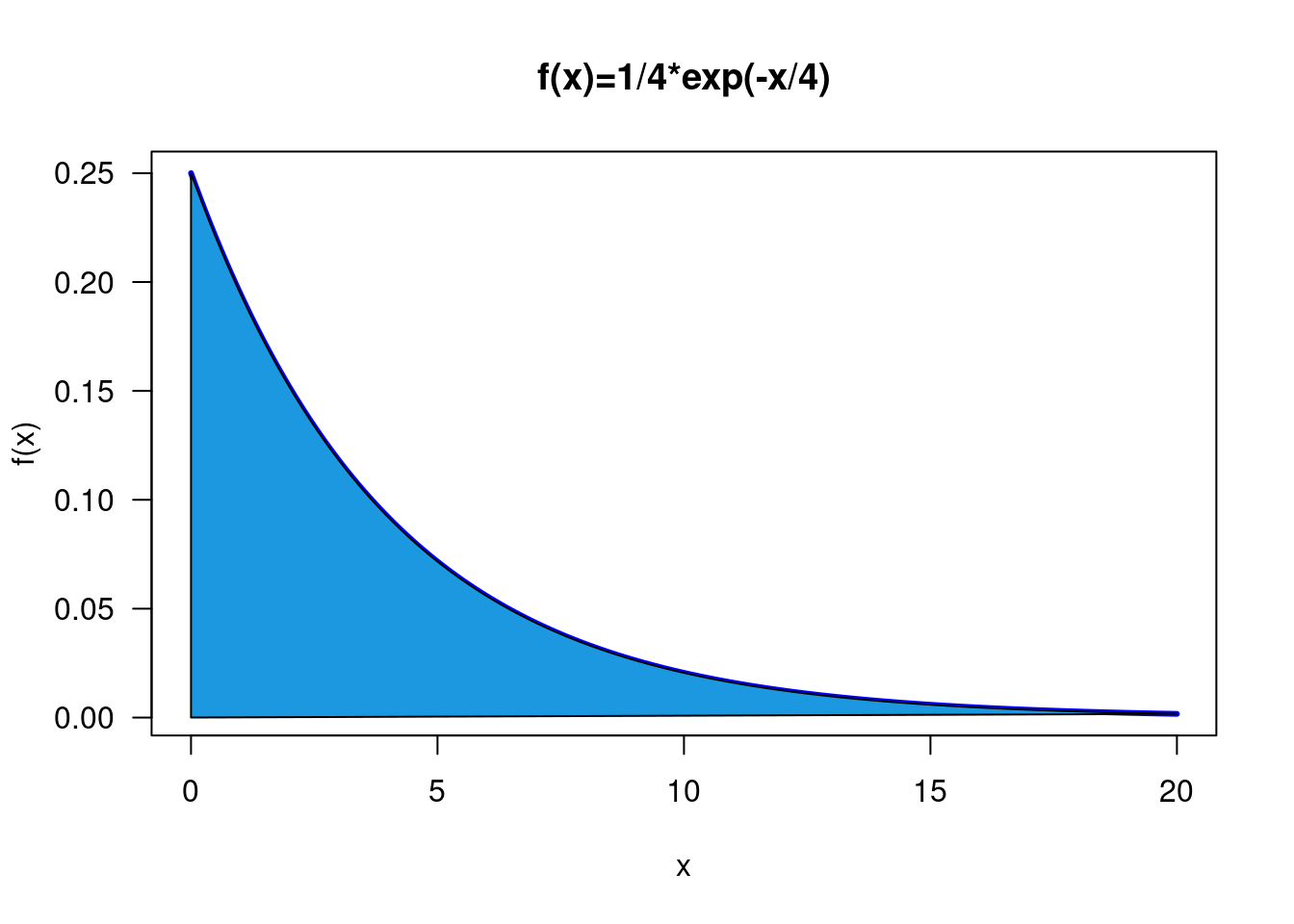


Si se requiere una parte sombreada reducimos el rango de los dos conjuntos

x=seq(from = 0, to = 20, by = 0.1)
y=function(y){1/4*exp(-y/4)}
fx=y(x)
plot(x,fx, xlab="x", ylab="f(x)", type="l",
             col="blue", lwd=3, main="f(x)=1/4*exp(-x/4)", las=1  )
x1=seq(from=0, to=5,by=0.1)
fx1=y(x1)
x1=c(0,x1,5)
fx1=c(0,fx1,0)
polygon(x1, fx1,col = "#4876FF")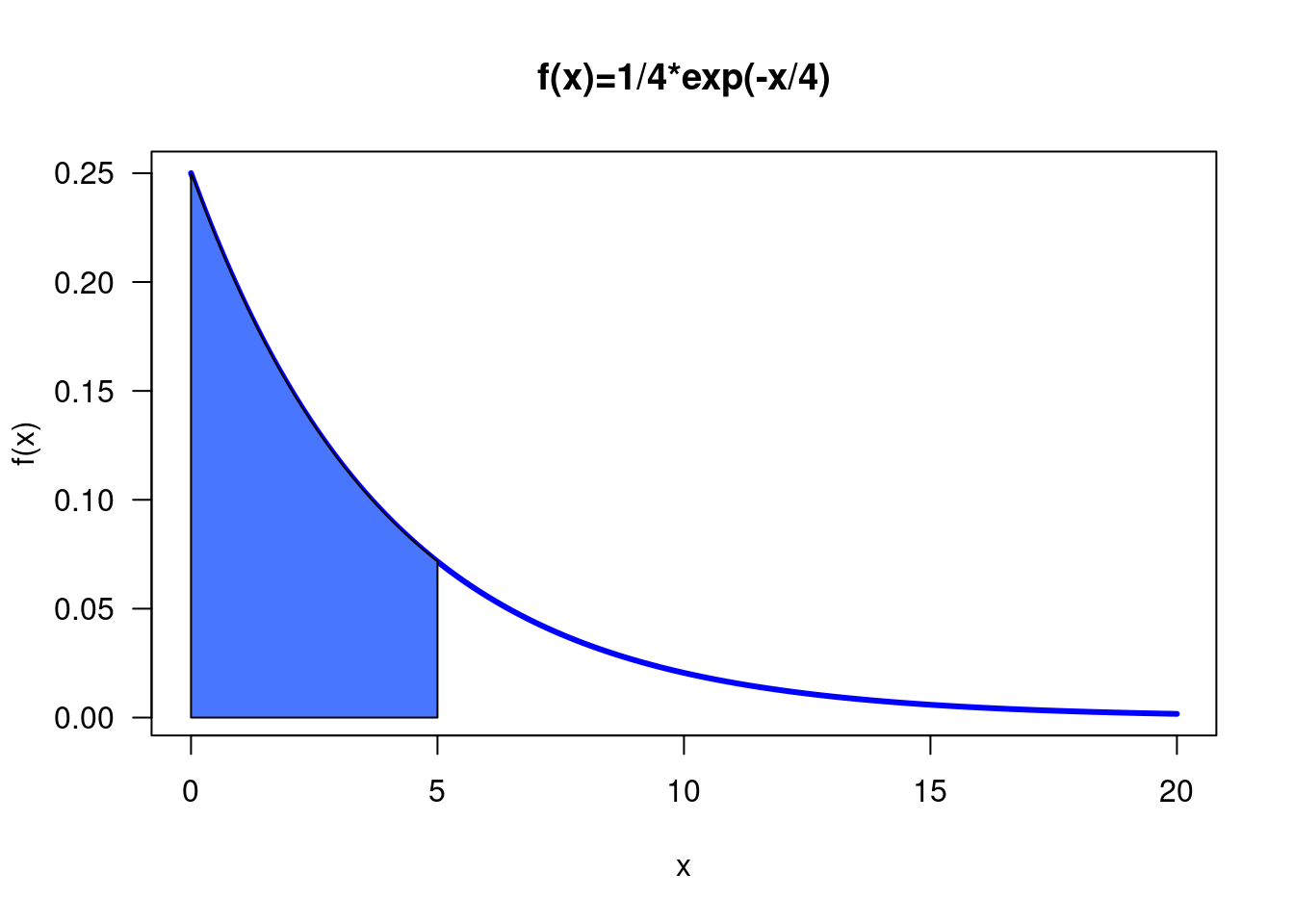



Se puede utilizar la libreria de ggplot2

library(ggplot2)
ggplot(data.frame(x=c(0, 20)), aes(x)) + 
    stat_function(fun=function(x){1/4*exp(-x/4)},colour="blue", size=1,
                  geom="area", fill="#4876FF", alpha=0.5)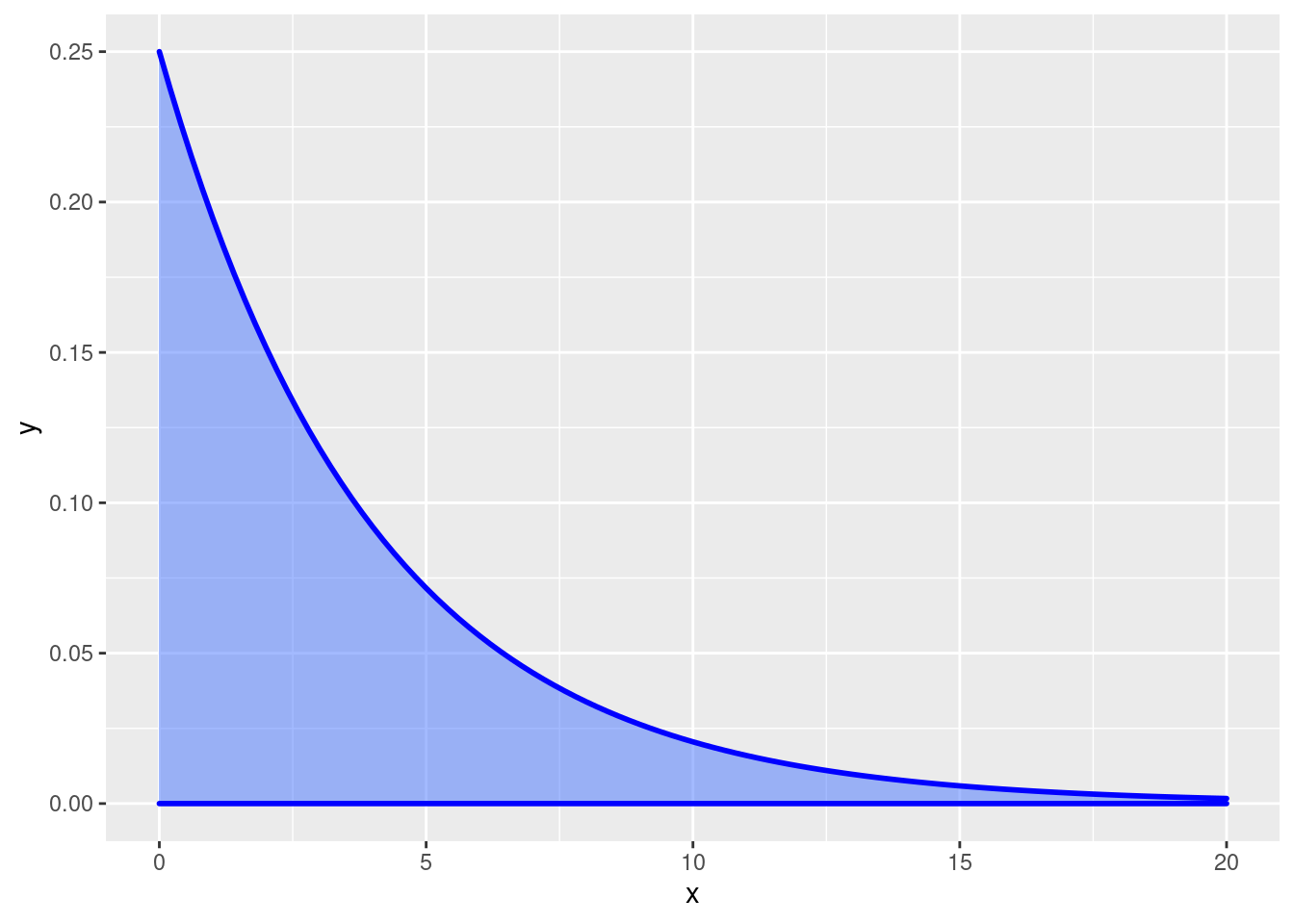



Integración


\(\displaystyle\int\limits_{0}^{+\infty} \dfrac{1}{4} e^{-y/4} \:dx\)

fy=function(y){1/4*exp(-y/4)}
integrate(fy, lower=0,upper=Inf)
1 with absolute error < 2.7e-05



https://ggplot2tutor.com/tutorials/sampling_distributions