Código 10
Módulo 5- Unidad 5.1
dgonzalez
Regresión Lineal Simple
x=c(24.3, 12.5, 31.2, 28.0, 35.1, 10.5, 23.2, 10.0, 8.5, 15.9, 14.7, 15.0)
y=c(16.2, 8.5, 15.0, 17.0, 24.2, 11.2, 15.0, 7.1, 3.5, 11.5, 10.7, 9.2)
plot(x,y, pch=19, col=c5, las=1)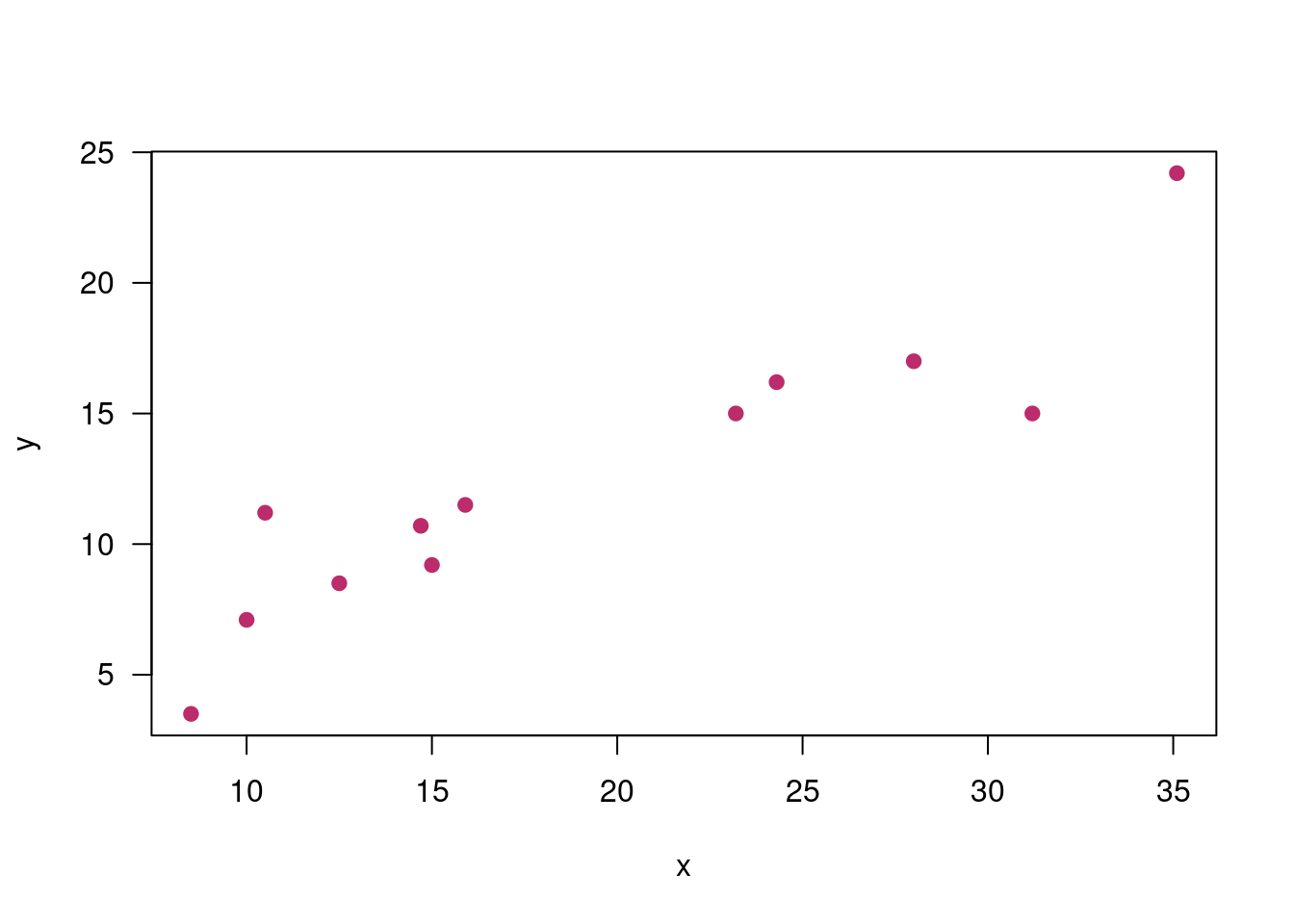
Estimación MCO
\(\widehat{y}= b_{0} + b_{1} x\)
regresion=lm(y ~ x)
summary(regresion)##
## Call:
## lm(formula = y ~ x)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.1928 -0.5426 0.0088 0.8500 3.5613
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.77788 1.58292 1.123 0.288
## x 0.55817 0.07567 7.376 2.38e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.251 on 10 degrees of freedom
## Multiple R-squared: 0.8447, Adjusted R-squared: 0.8292
## F-statistic: 54.41 on 1 and 10 DF, p-value: 2.38e-05plot(x,y, xlab = "Ingresos", ylab = "Consumo", pch=19, col=c5, las=1)
abline(regresion)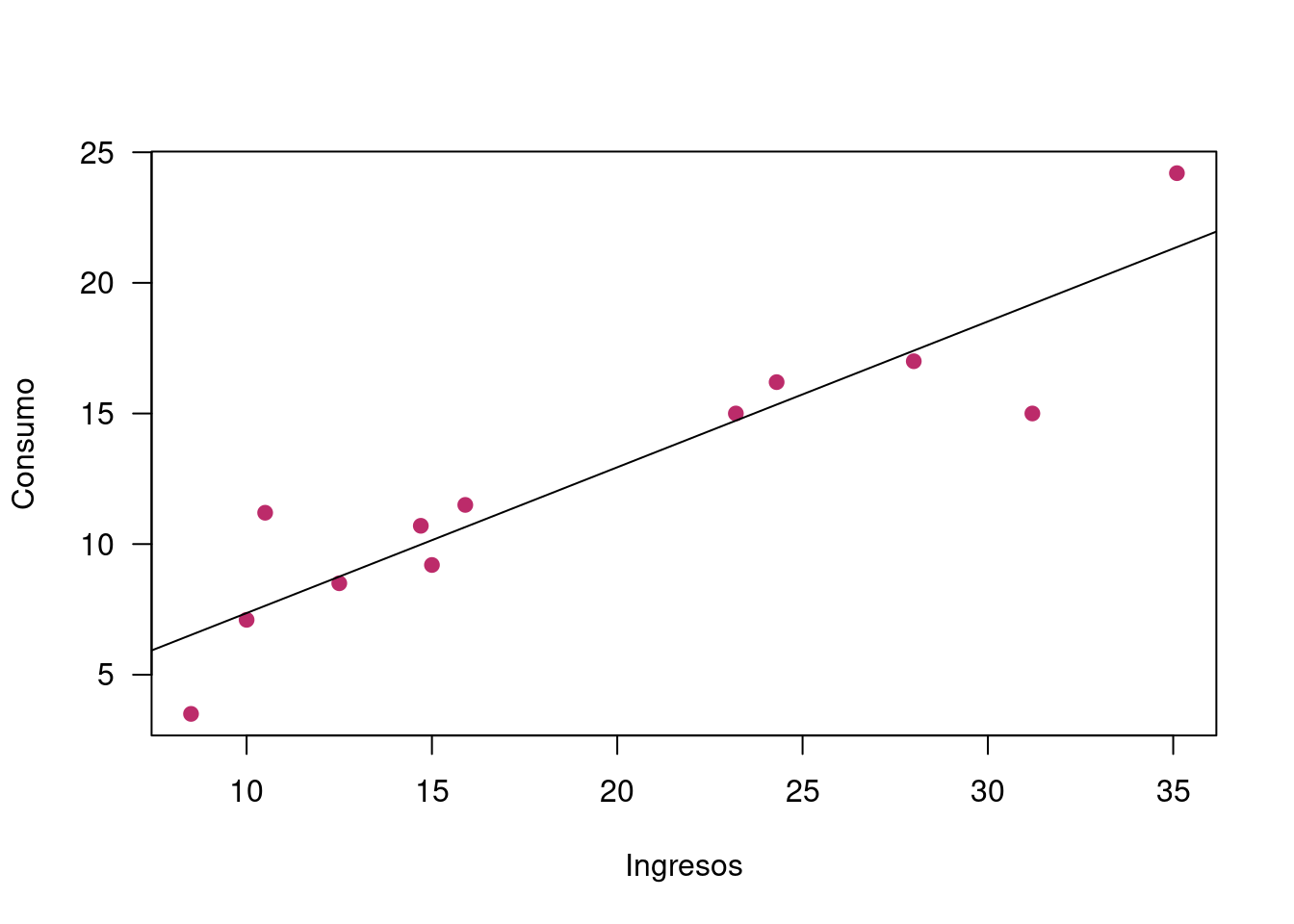
Estimaciones y Residuales
yhat=fitted(regresion) # guarda "y" estimada
uhat=regresion$residuals # guarda residuales
data.frame(x,y,yhat,uhat)## x y yhat uhat
## 1 24.3 16.2 15.341446 0.8585544
## 2 12.5 8.5 8.755023 -0.2550230
## 3 31.2 15.0 19.192828 -4.1928284
## 4 28.0 17.0 17.406680 -0.4066799
## 5 35.1 24.2 21.369697 2.8303031
## 6 10.5 11.2 7.638680 3.5613199
## 7 23.2 15.0 14.727457 0.2725429
## 8 10.0 7.1 7.359594 -0.2595944
## 9 8.5 3.5 6.522337 -3.0223373
## 10 15.9 11.5 10.652806 0.8471942
## 11 14.7 10.7 9.983000 0.7169999
## 12 15.0 9.2 10.150451 -0.9504515plot(x,yhat, xlab = "Ingresos", ylab = "Consumo estimado", pch=19, col=c3, las=1)
abline(regresion)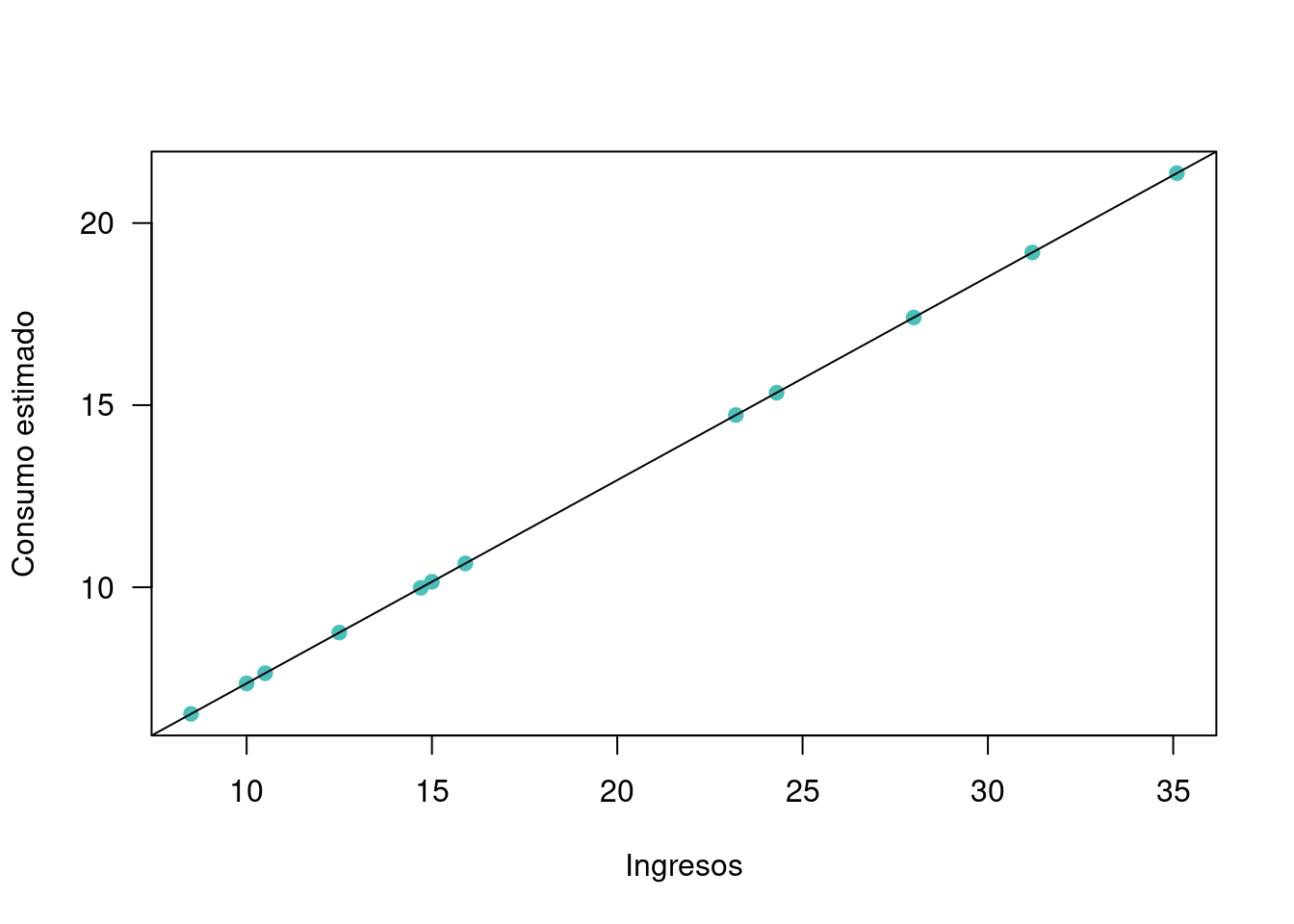
Validación de supuestos
Supuesto 1
# Test de normalidad de los errores
# Ho: los errores tienen distribución normal
ks.test(uhat, "pnorm") # test de normalidad##
## One-sample Kolmogorov-Smirnov test
##
## data: uhat
## D = 0.17998, p-value = 0.7698
## alternative hypothesis: two-sidedshapiro.test(uhat) # test de normalidad##
## Shapiro-Wilk normality test
##
## data: uhat
## W = 0.94569, p-value = 0.5751# se debe instalar paquete fBasics
# install.packages("fBasics")
library(fBasics)
jarqueberaTest(uhat) # test de normalidad##
## Title:
## Jarque - Bera Normalality Test
##
## Test Results:
## STATISTIC:
## X-squared: 0.2039
## P VALUE:
## Asymptotic p Value: 0.9031
##
## Description:
## Fri Jan 7 19:45:42 2022 by user:Supuesto 2
# t-test para verificar E[u]=0, modelo completo
# Ho: miu_u = 0
t.test(uhat)##
## One Sample t-test
##
## data: uhat
## t = -5.9676e-17, df = 11, p-value = 1
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
## -1.363421 1.363421
## sample estimates:
## mean of x
## -3.696678e-17Supuesto 3
# Test de Autocorrelacion de errores
# Cor[ui,uj]=0
# Ho: no existe autocorrelacion entre los errores
# se debe instalar paquete lmtest
# install.packages("lmtest")
library(lmtest) #dwtest
dwtest(y ~ x) # test de Durbin-Wapson##
## Durbin-Watson test
##
## data: y ~ x
## DW = 1.5517, p-value = 0.1769
## alternative hypothesis: true autocorrelation is greater than 0Supuesto 4
# Test de Homoscedasticidad
# Ho: la varianza de los erroes es constante
# Ho: V(u) = sigma2
gqtest(y ~ x)##
## Goldfeld-Quandt test
##
## data: y ~ x
## GQ = 0.19285, df1 = 4, df2 = 4, p-value = 0.93
## alternative hypothesis: variance increases from segment 1 to 2library(ggplot2)
x=c(24.3, 12.5, 31.2, 28.0, 35.1, 10.5, 23.2, 10.0, 8.5, 15.9, 14.7, 15.0)
y=c(16.2, 8.5, 15.0, 17.0, 24.2, 11.2, 15.0, 7.1, 3.5, 11.5, 10.7, 9.2)
datos=data.frame(x,y)
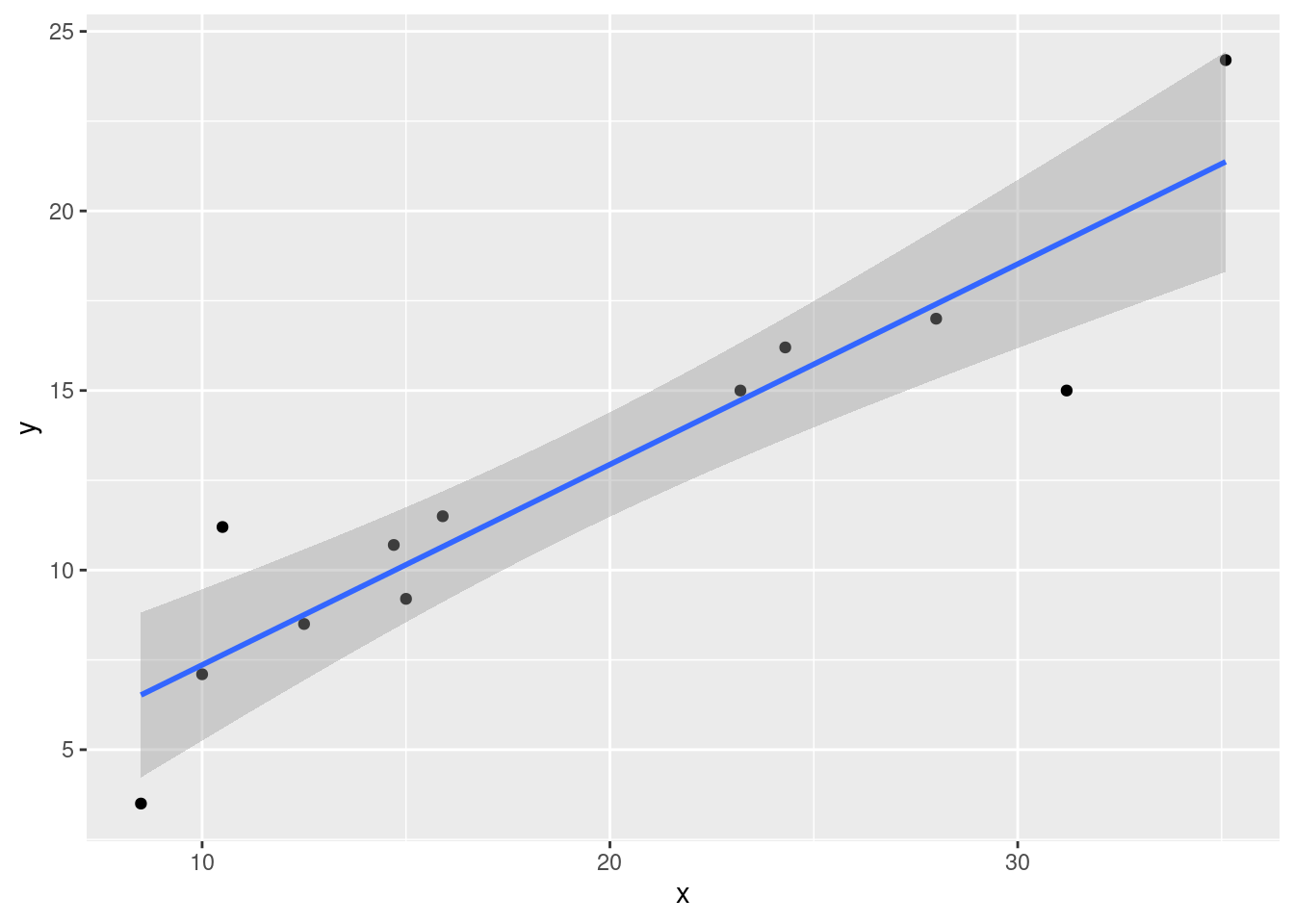
p <- ggplot(datos, aes(x, y)) +
geom_point()
p + geom_smooth(method = "lm", level = 0.95)